Comparing Features of High- and Low-Rated Mathematics Lessons
Posted on

This blog post was written by Nanette Seago, Senior Program Associate for the Science, Technology, Engineering, & Mathematics program, and Rebecca Perry, Senior Program Associate for the Innovation Studies program.
Together with our WestEd research colleagues,* we visited almost 50 elementary and middle school classrooms in eight California school districts during the 2015/16 academic year to observe and analyze mathematics lessons.
These classroom observations were part of our formative evaluation of Math in Common (MiC), an initiative supporting a network of 10 California school districts as they implement the Common Core State Standards in Mathematics (CCSS-M) across grades K–8.
We were specifically interested in examining shifts in teachers’ instructional practices related to CCSS-M, and learning whether there were instructional patterns to be found within and across the MiC districts.
We found that there is a wide variation in the degree to which teachers empower students to own their thinking and work at every stage of a math lesson.
Based on this and other findings from our observations, we developed composite lesson outlines that describe the major segments that made up teachers’ lessons.
Figure 1 displays two outlines of these composite lessons: the first composite lesson outline is based on five lessons that received relatively high ratings on our observation rubric and the second composite outline is based on five lessons that received relatively low ratings.
The figure highlights differences between the high- and low-rated lessons regarding: (1) the number of lesson segments (shown by the colored bars) and (2) the amount of time allocated for different lesson segments (shown by the percentages of the whole for each segment).
As seen in the figure below, the high-rated lessons comprised five main lesson segments, while the low-rated lessons comprised three main segments.
Figure 1. Outlines of “high-rated” and “low-rated” composite lessons (Spring 2016)
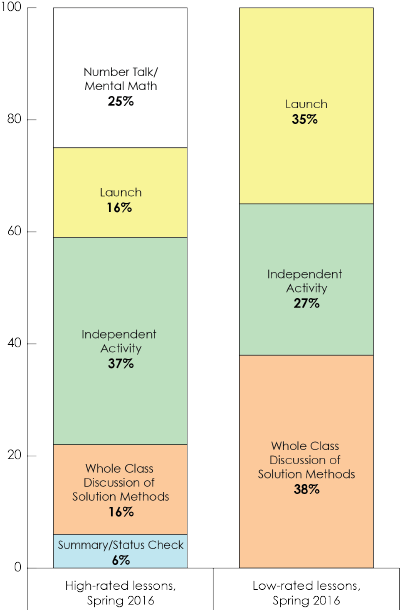
Both the high- and low-rated composite lessons roughly followed what we categorized as a Launch–Explore–Summarize structure, but there appeared to be a fair amount of variation between them. Launch-Explore-Summarize is a common instructional approach in mathematics classrooms where teachers “launch” the lesson by giving students information needed to do the lesson and solve the task and then allow students time to “explore” the mathematics of the task or lesson on their own or in groups. The main teaching during the lesson occurs in the “summarize” portion of the lesson, when students are brought back together to explain their solutions as the teacher facilitates to ensure that the lesson meets the overall mathematical goals.
Variation in Launch activities
The Launch portion of the lessons varied across the teachers we observed, both in terms of time devoted and nature of the mathematical activity. As a result, we found widely differing opportunities for students to own the intellectual work, and these opportunities formed the basis of the high or low ratings.
- The Launch portion of the lesson in the low-rated group was more extended than in the high-rated group and often included teacher-driven activities like vocabulary review, example problems, and review of prior knowledge.
- All of the high-rated lessons included a Number Talk or Mental Math activity preceding the lesson launch, which teachers used to elicit student reasoning, explanations, and mathematical sense-making in order to get students “warmed up” to do some deep mathematical thinking. (None of the low-rated lessons included those types of pre-Launch activities.)
Variation in Explore activities
We also found differences in the way the Explore portion was structured between the two composites.
- In the low-rated group, the teachers tended to direct students to work together on procedural worksheets or handouts. Students had only scattered opportunities to offer explanations of their thinking or compare multiple procedures or representations.
- In the high-rated group, the Explore activities tended to allow students to work together on problems and to share and discuss (and often compare) their thinking, followed by some whole-class discussion of the solutions. In some cases, teachers also provided opportunities for students to attempt to solve problems individually prior to discussions with their peers.
Variation in Summarize activities
- In the low rated group, for the final Summarize phase of the lesson there tended to be no summary of the lesson at all, and little or no discussion or comparison of student approaches at the end of the lesson. In many cases, the lessons stopped when the bell rang, with little closure in the mathematical learning for students.
- In the high-rated group, teachers frequently led at least a brief summary of the key learnings from the lesson.
To all the teachers and administrators involved in math instruction, we wonder how these composite lessons compare with math lessons in your district. Based on your own observations of classroom instruction, do these high- and low-rated composite lessons resonate with what you’ve seen in your elementary and/ or middle school classrooms, or are you seeing something different in your district? We hope these composite lessons provide fodder for thinking about how to structure and sequence effective math lessons as teachers implement the CCSS-M and other state standards.
We’d love to hear from you. Please leave a comment on this post, send us an email at mic@wested.org or go to Nanette’s profile page, click Contact by email, and send a comment.
*Cathy Carroll, Frances Reade and Haiwen Chu were members of the observation team who prepared an internal summary of our 2015/16 observations for our district partners.
